or, Scope-sensitive snafus in summing speculations

(1)

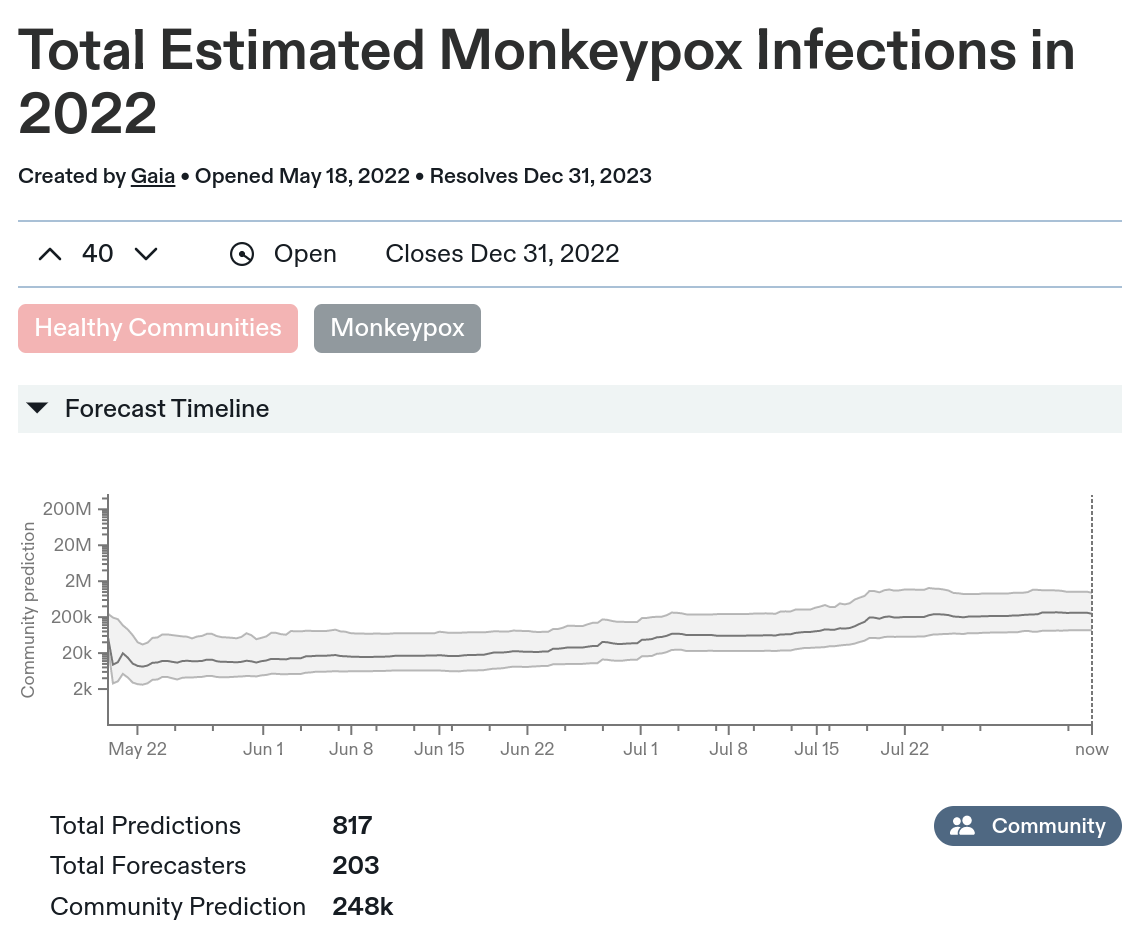
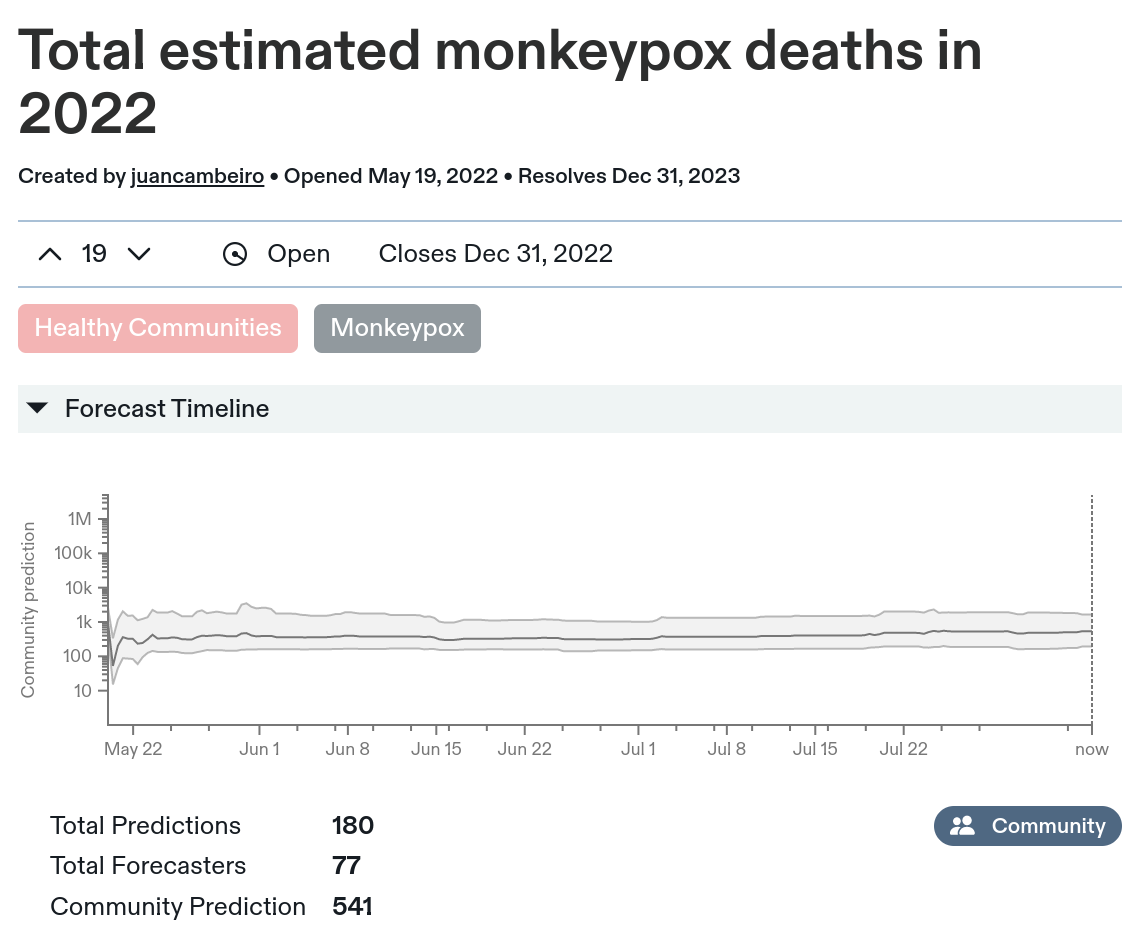
Should I expect monkeypox to be a big deal for the world? Well, fortunately, Metaculus has a pair of questions that ask users to predict how many infections and deaths there will be in 2022:

203 users(!) made 817 predictions of infections, and Metaculus helpfully aggregates those into a "community prediction" of ~248k infections. 77 users made 180 predictions of deaths, with a community prediction of 541.

The y-axis is on a log scale (as are the predictors' distributions). This is a good choice! Whatever you expect the most-likely case to be, there's definitely a chance with things like this that one a misestimation or shift in one factor can make it bigger or smaller by a multiple, not just an additive amount.

What's not a good choice is to report the median outcome of the aggregate position as the "community prediction". This causes a headline

(1)

The following proposition is paraphrased from Savage 1971 (pdf), the original paper that introduced proper scoring rules way back when. Savage characterized the space of all possible scoring rules two ways -- in the now-common form using a general convex function and its subgradient, and in the equivalent "schedule of demands" form that has a natural interpretation as being given the opportunity to trade into a limit order book.

Proposition 1. Any (strictly) proper scoring rule \(S(p,q)\) can be written as \(S(p,q):=\alpha+S^*(p,q)\), where \(\alpha\in\mathbb R\) is a constant and \(S^*(p,q)\) is the profits-or-losses from trading into a limit order book (with nonzero size available at each price) when your initial position is some \(\beta\), your fair value is \(p\), and the contract value resolves to \(q\).

Proof. Let \(\phi:[0,1]\to\mathbb R\) be a

In Zvi's 2/11 Covid update, he turned to Metaculus for help. He looked at the numbers. Becase the man is an inveterate trader, he saw odds that were Wrong On The Internet and just couldn't stop himself from creating an account to bet against it. And then he saw the payout structure and decided he was done after making a single prediction.

I spent some time with the Metaculus site and figured out how they borked this one up enough to drive away Zvi Mowshowitz. I'll try to explain it here.

(1)

Here's a presumably current description of the scoring function that I found on the FAQ, slightly abridged:

Your score \(S(T;f)\) at any given time \(T\) is the sum of an "absolute" component and a "relative" component: \[S(T;f)=a(N)\times L(p;f)+b(N)\times B(p;f),\] where \(N\) is the number of predictors on the question.

If we define \(f=1\) for a positive resolution of the question and \(f=0\) for a negative resolution, then \(L(p;f)=\log_2(p/0.5)\) for \(f=1\) and \(L(p;f)=\log_2((1−p)/0.5)\) for

(1)

Political betting site PredictIt offers everyone the ability to (legally) bet (real money) on the outcome of political events. For example:

You can pay 39¢ for a Yes share in BUSH.RNOM16, which will be worth $1 if Jeb Bush wins the Republican nomination, and $0 if he does not. Similarly, you can pay 63¢ for a No share in BUSH.RNOM16, which will be worth $0 if he wins and $1 otherwise. (Another way to think about this is that you can sell a Yes share for 37¢ or buy one for 39¢. These numbers are different for pretty much the same reason that you can't sell your used textbooks